Getting Started on a Model for Tendon-driven Continuum Robots

As you’ve been reading so far, there are multiple facets to continuum robot modeling. We will pick up this thread today and follow it into the world of modeling tendon-driven continuum robots. We will be narrowing our focus on modeling the forward mapping from actuation inputs such as tendon tension or displacements to the final backbone shape in task space.

Before we start our journey into the rabbit-hole, a quick refresher can be found in these prior posts on constant curvature (CC) representation and its associated kinematic model.

Three Steps to a Model

There are three major steps to designing the right model for a tenon-driven continuum robot for your purposes:

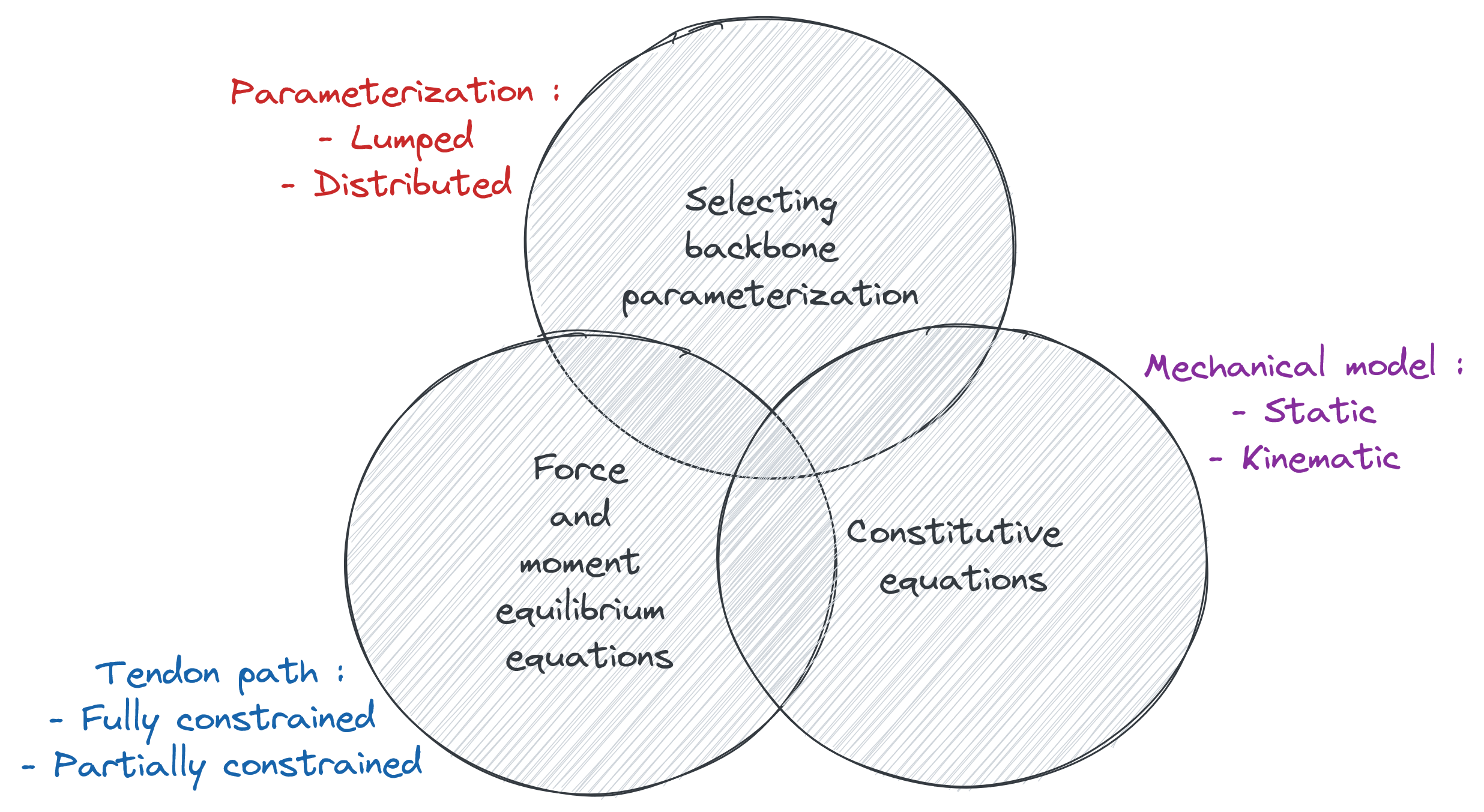
Step 1: Selecting the Backbone Parameterization

Selecting a parameterization determines the configuration space, and consequently its mapping to the task space for the robot. The available representations can be classified as either distributed or lumped.

• Distributed parameterization represents the backbone as a continuous curve that are expressed as a function of the distance along the backbone

• Lumped parameterization discretizes the curve using geometrical assumption such that the curve can be represented by a finite number of parameters. The CC representation we saw in an earlier post falls under this category.

Step 2: Deriving the Force and Moment Equilibrium Equations

Doing so requires us to decide the shape of tendon path we’d like to consider.

• Fully constrained tendon path assumes that the tendons run parallel to the backbone and are represented by continuous curves

• Partially constrained tendon path assumes that the tendons are constrained at discrete locations, and therefore can be represented by a series of line segments.

If a kinematic model is chosen, then the shape of the tendon path will determine the mapping between the joint and configuration space. A static model will have the tendon path influence both the mapping as well as the computed tendon force interactions.

Step 3: Writing the Constitutive Equations

Choosing between a static or kinematic model depends on the factors required to be modeled such as external force, gravity etc.

• A purely kinematic model uses robot geometry to derive the constitutive equations. The robot geometry enforces constraints on the robot shape that can be used to solve for the unknown parameters.

• A static model will consider the robots material properties and tendon interactions to model its shape. Generally, the backbone is assumed to experience elastic strains and modeled using the Hooke’s law, where the developed stress is directly proportion to its strain. A static model can account for external forces and moments.

The steps described above largely follow our review paper ¹, where we classified different modeling approached based on the backone parameters required to define the backbone and the assumed tendon path.

Classification of different modelling approaches based on the backbone parameters required to define the backbone and assumed tendon path.

Getting Started with Your TDCR Model

Before you spiral into decision fatigue over the different options you can choose from, the foremost factor to consider is the tradeoff between accuracy and computation time that best suits our application. The more number of physical phenomenon that are considered, the more accurate the ensuing model. However, this might also entail a tradeoff on the computation time. In the second half of our review paper¹, we analyse this tradeoff for some common models in the literature with in-depth analysis and summary for your reference.

We provide open-source code of all the models we use for the analysis in our review paper ¹ on GitHub:

Both, C++ and Matlab implementations are available for a two segment TDCR, where the robot parameters can be varied based on your application. The following models are provided:

• A geometry based modeling approach assuming constant curvature bending for each segment (Constant Curvature Model) ²

• A static modeling approach modeling assuming constant curvature bending for each subsegment, i.e. between neighbouring disks (Piecewise Constant Curvature Model) ³

• A static modeling approach modeling each subsegment as a pseudo rigid body with virtual discrete joints (Pseudo Rigid Body Model) ¹ (Proposed independently in our paper)

• A static modeling approach modeling each segment as a Cosserat rods subject to tendon loads (Cosserat Rod Model) ⁴

• A static modeling approach modeling each subsegment, i.e. between neighbouring disks, as a Cosserat rod subject to tendon loads (Subsegment Cosserat Rod Model) ⁵

Resources: Our review paper and repository are great resources to get started on your modeling journey for tendon-driven continuum robots. Paper GitHub

If you would like to contribute to the TDCR modeling repository with your own implementation of other models in literature, please get in touch! We would love to improve the existing arsenal of models provided to the community.

References

1. P. Rao, Q. Peyron, S. Lilge, J. Burgner-Kahrs: How to Model TendonDriven Continuum Robots and Benchmark Modelling Performance. Frontiers in Robotics and AI, vol. 7, p. 223, 2021. doi: 10.3389/frobt.2020.630245 ↩ ↩² ↩³ ↩⁴

2. R. J. Webster and B. A. Jones: Design and kinematic modeling of constant curvature continuum robots: A review. International Journal of Robotics Research, vol. 29, no. 13, pp. 1661–1683, 2010. doi: 10.1177/0278364910368147 ↩

3. H. Yuan, L. Zhou, W. Xu: A comprehensive static model of cable-driven multi-section continuum robots considering friction effect. Mechanism and Machine Theory, vol. 135, pp. 130–149, 2019. doi: 10.1016/j.mechmachtheory.2019.02.005 ↩

4. D. C. Rucker and R. J. Webster: Statics and dynamics of continuum robots with general tendon routing and external loading. IEEE Transactions on Robotics, vol. 27, no. 6, pp. 1033–1044, 2011. doi: 10.1109/TRO.2011.2160469 ↩

5. A. Gao, Y. Zou, Z. Wang, H. Liu: A general friction model of discrete interactions for tendon actuated dexterous manipulators. Journal of Mechanisms and Robotics, vol. 9, no. 4, 2017. doi: 10.1115/1.4036719 ↩