Oren Salzman

Oren Salzman

Assistant Professor.

Algorithmic Motion Planning Meets Minimally-Invasive Robotic Surgery

5 minute read

A Case Study of Steerable Needles

Steerable needles are a type of continuum robot, distinguished by their flexibility and capability to navigate through complex anatomical pathways. These robots are highly under-actuated, relying on interaction with the environment for movement and direction. The steering mechanism of steerable needles utilizes the asymmetric tip’s interaction with tissue forces during insertion. By externally rotating the needle shaft, the tip’s orientation is adjusted, allowing for controlled deflection towards desired directions upon further insertion. This method enables the needle to maneuver around obstacles such as bones, vessels, and nerves, accessing multiple targets without complete withdrawal. The reliance on environmental interaction for actuation not only enhances the safety and efficacy of medical interventions but also presents challenges and opportunities in motion planning and control within robotics, emphasizing navigation in environments with complex constraints and precision requirements.

Motion Planning for Steerable Needles

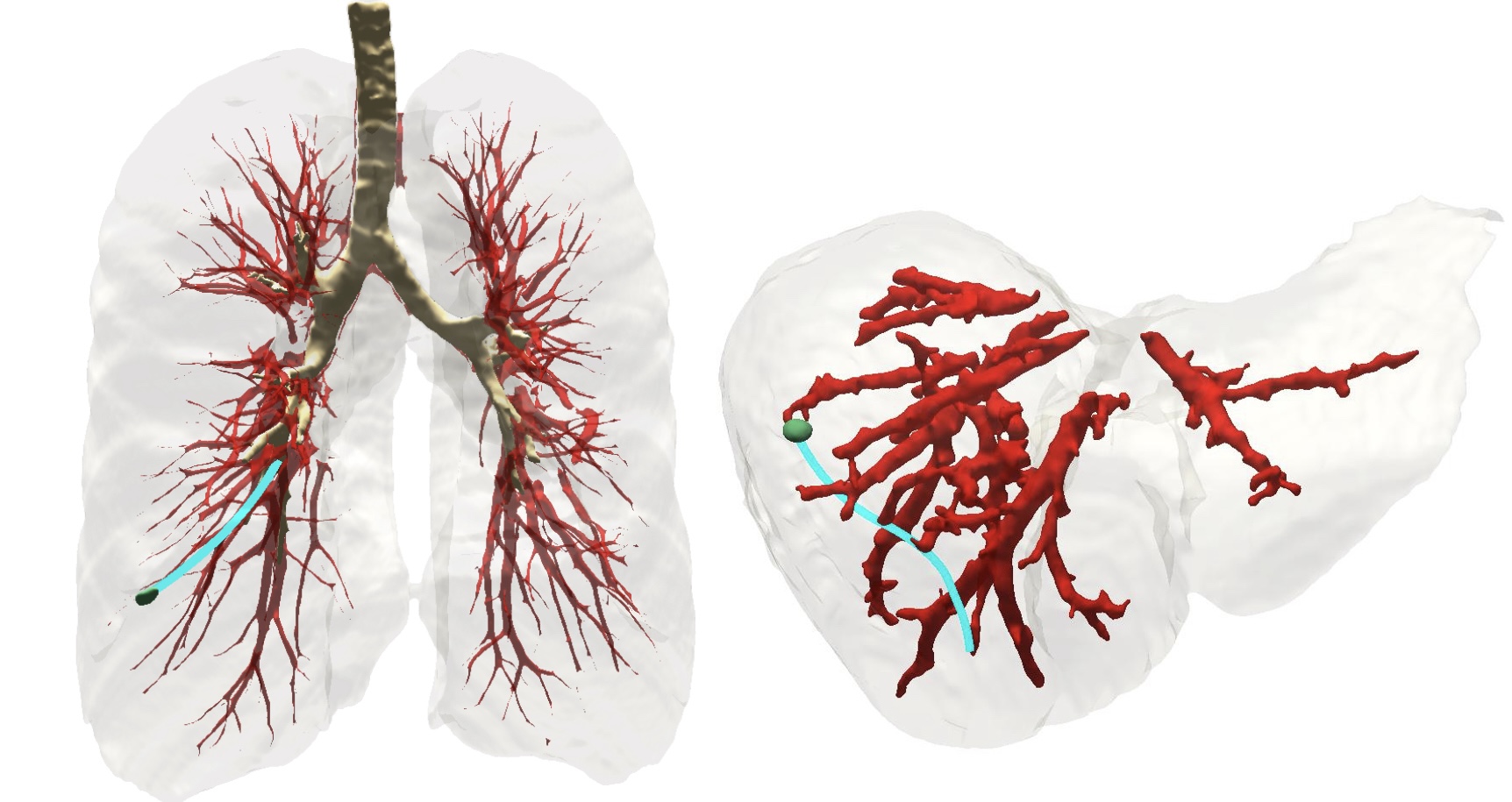
Steerable needles can be used to reach clinical targets for biopsy purposes while safely avoiding obstacles such as blood vessels. This clinical application can be modeled as a motion-planning problem which is the problem of determining a collision-free path or trajectory for a robot to move from its initial position to a desired goal position while avoiding obstacles in its environment (see also previous motion planning posts Part 1, Part 2).

A medical steerable needle (cyan) is used to reach a nodule (green) while avoiding major blood vessels (red) for biopsy or cancer treatment. The left and right figures depicts the lung parenchyma (where the bronchial tubes are in brown) and the liver, respectively.

Ideally, a motion-planning algorithm should first guarantee that it will compute a solution, if one exists, in finite time, or notify the user that no solution exists (we call such motion planners complete”). Moreover, the computed solution should strive to maximize some objective which in our setting is patient safety (we call such motion planners optimal). This can be quantified using metrics such as minimizing trajectory length, maximizing the minimal distance from obstacles and minimizing damage to sensitive tissue (see, e.g., 1 2 3 4). Unfortunately, the lion’s share of planners developed for steerable needles offer no formal guarantee on completeness, let alone optimality.

Some prior motion planners for steerable needles (see, e.g, 5 6 7) do aim to optimize motion-plan cost but they lack global optimality guarantees (this means that the cost of the solution they return may be a local optima). Some sampling-based planners (see, e.g., 8 9) are known to be both complete and optimal but those properties are usually proven only when they number of samples they use approaches infinity (this is referred to as asymptotic optimality).

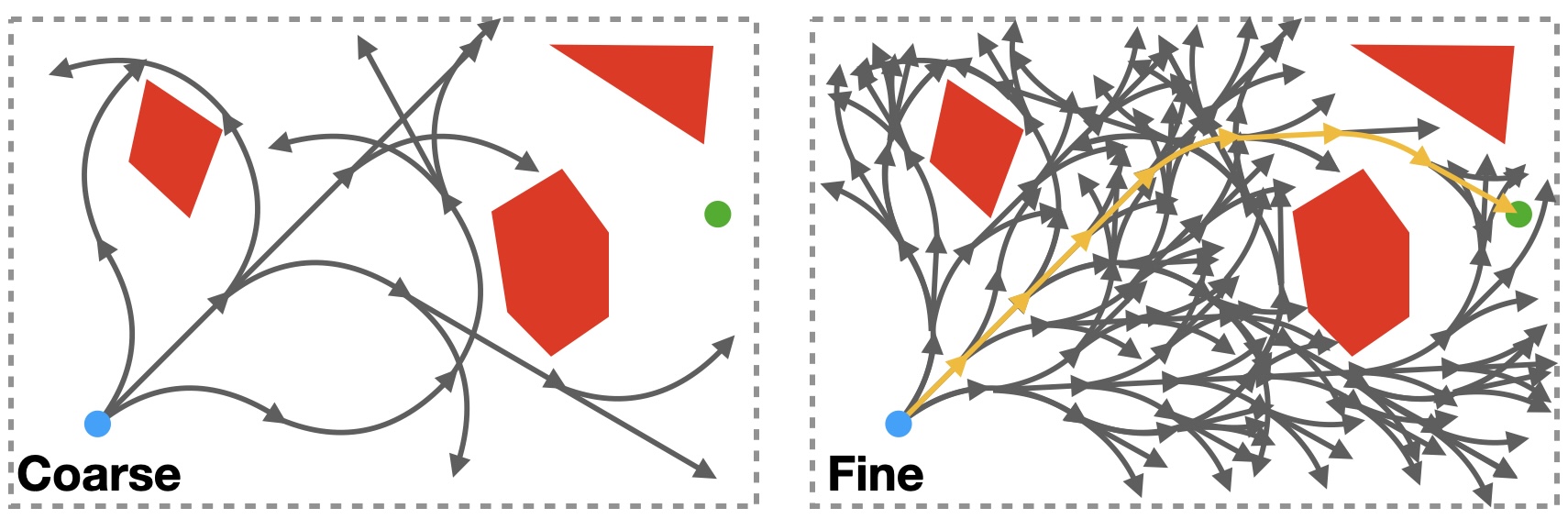
These challenges inspired us to consider variants of completeness or optimality relevant to medical applications: In a series of recent papers (see, 10 11), we focus on specific types of guarantees relevant to real-world medical applications: resolution completeness and resolution optimality. Generally speaking, a resolution characterizes the discretization of some space such as the action space or configuration space of a robot. An algorithm is resolution complete if there exists a fine-enough resolution with which the algorithm finds a plan in finite time when a qualified solution exists, and otherwise correctly returns that no such plan exists. An algorithm is resolution optimal if it is resolution complete and if, when it does return a motion plan, the plan’s cost is guaranteed to be within a desired approximation factor of the cost of a globally optimal qualified motion plan. We illustrate this in the Figure below with an example showing searches with different resolutions for needle steering.

Our resolution-complete motion planner uses search trees built using different resolutions, illustrated here in 2D. A valid motion plan goes from the start configuration (blue dot) to the goal point (green dot), while avoiding obstacles (red) and satisfying kinematic constraints. The left search tree uses a coarse resolution and fails to find a plan while the right one uses a finer resolution and successfully generates a motion plan (yellow).

We first presented Resolution-Complete Search (RCS), an efficient, resolution-complete motion planner for steerable needles based on a novel adaptation of multi-resolution planning 8. Under some mild assumptions on the system and the solution, the planner, in finite time, is guaranteed to find a plan as long as the problem admits a qualified solution. We then extended RCS to develop RCS*, that achieves resolution optimality 9.

We demonstrated the performance of our planners in two clinically realistic scenarios where the needle should reach a target while safely avoiding obstacles (e.g., blood vessels). In the setting of lung biopsy, where the needle is deployed through a bronchoscope and must steer through the lung parenchyma (the tissue of the lung outside the bronchial tubes) and in the setting of liver biopsy, where the needle is deployed into the liver through its anterior surface and must steer through the liver tissue. We compared in simulation our planner with several other steerable needle planners and demonstrated experimentally that RCS and RCS* outperform the state-of-the-art in terms of computation time, success rate, and plan quality.

For additional details on algorithmic motion planning for continuum robots, see 12 and references within.

References

  1. Alberto Favaro, Leonardo Cerri, Stefano Galvan, Ferdinando Rodriguez Y Baena, and Elena De Momi. Automatic optimized 3D path planner for steerable catheters with heuristic search and uncertainty tolerance. IEEE ICRA, pp 9–16, 2018. doi: 10.1109/ICRA.2018.8461262 ↩

  2. Alan Kuntz, Luis G Torres, Richard H Feins, Robert J Webster III, and Ron Alterovitz. Motion planning for a three-stage multilumen transoral lung access system. IEEE IROS, pp 3255–3261, 2015. doi: 10.1109/iros.2015.7353829 ↩

  3. Mengyu Fu, Alan Kuntz, Robert J Webster III, and Ron Alterovitz. Safe motion planning for steerable needles using cost maps automatically extracted from pulmonary images. IEEE IROS, pp 4942–4949, 2018. doi: 10.1109/IROS.2018.8593407 ↩

  4. Michael Bentley, Caleb Rucker, Chakravarthy Reddy, Oren Salzman, Alan Kuntz. Safer Motion Planning of Steerable Needles via a Shaft-to-Tissue Force Model. J. Medical Robotics Res. 8(1&2): 2350003:1-2350003:16, 2023. doi: 10.1142/S2424905X23500034 ↩

  5. Jijie Xu, Vincent Duindam, Ron Alterovitz, and Ken Goldberg. Motion planning for steerable needles in 3D environments with obstacles using rapidly-exploring random trees and backchaining. IEEE CASE, pp 41–46, 2008. doi: 10.1109/COASE.2008.4626486 ↩

  6. Sachin Patil, Jessica Burgner, Robert J Webster III, and Ron Alterovitz. Needle steering in 3D via rapid replanning. IEEE Trans. Rob., 30(4):853–864, 2014. doi: 10.1109/TRO.2014.2307633 ↩

  7. Marlene Pinzi, Stefano Galvan, and Ferdinando Rodriguez y Baena. The adaptive hermite fractal tree (AHFT): a novel surgical 3D path planning approach with curvature and heading constraints. International Journal of Computer Assisted Radiology and Surgery, 14(4):659–670, 2019. doi: 10.1007/s11548-019-01923-3 ↩

  8. Steven M LaValle. Planning algorithms. Cambridge university press, 2006. ↩ ↩2

  9. Oren Salzman. Sampling-based robot motion planning. Commun. ACM, 62(10):54–63, 2019. doi: 10.1145/3318164 ↩ ↩2

  10. Mengyu Fu, Oren Salzman, and Ron Alterovitz. Toward certifiable motion planning for medical steerable needles. In RSS, 2021. ↩

  11. Mengyu Fu, Kiril Solovey, Oren Salzman, and Ron Alterovitz. Resolution-optimal motion planning for steerable needles. IEEE ICRA, pp 9652–9659, 2022. doi: 10.1109/ICRA46639.2022.9811850 ↩

  12. Oren Salzman. Algorithmic Motion Planning Meets Minimially-Invasive Robotic Surgery. IJCAI,pp 7039-7044, 2023. doi: 10.24963/ijcai.2023/804 ↩

Categories:

Updated: